Illustration of the static dependence graph used by Diver

How Diver Works

The core technique of Diver is the trace-pruning algorithm based on a fine-grained static dependence graph. This page illustrates the Diver dependence graph with an example Java program as follows.

Example Program

/* example code for Diver */
public class A {
	static int g; public int d;
	String M1(int f, int z) {
		int x = f + z, y = 2, h=21;
		if (x > y) {
			M2(x,y);
		}
		int r = new B().M3(h,g);
		String s = "M3 retval: " + r;
		return s;
	}

	void M2(int m, int n) {
		int t = m - d;
		if (t > 0) {
			n = g/t;
		}
		boolean b = C.M5(this);
		//System.out.println(b);
	}
}

/* example code for Diver */
public class B {
	static short t;

	int M3(int a, int b) {
		int j = 0; 
		t = -250;
		
		if ( a < b ) {
			j = b - a;
		}
		return j;
	}

	static double M4() {
		int x = A.g, i = 5;

		try {
			A.g = x/(i+t);
			new A().M1(i, t);
		}
		catch(Exception e) {	}

		return x;
	}
}

/* example code for Diver --- this is the entry class */
public class C {
	static void __link() { 
		Diver.EAMonitor.__link(); 
	}
	
	public static boolean M5(A q) {
		long y = q.d;
		boolean b = B.t > y;
		q.d = 2;
		return b;
	}

	public static void main(String[] args) {
		int a = 0, b = -3;
		String s = new A().M1(a,b);
		double d = B.M4();
		String u = s + d;
		System.out.println(u);
	}
}

the Diver dependence graph of the Example Program above

Data-dependence edges are labeled with the associated variables and the edge types separated with a colon. The data-dependence edge types are:

• p -- parameter edge
• r -- return edge
• h -- heap edge

Control-dependence edges are not labeled. Yet, line styles are used in this illustration to distinguish data and control dependencies:

• solid line -- interprocedural data dependence edge
• dashed line -- interprocedural control dependence edge

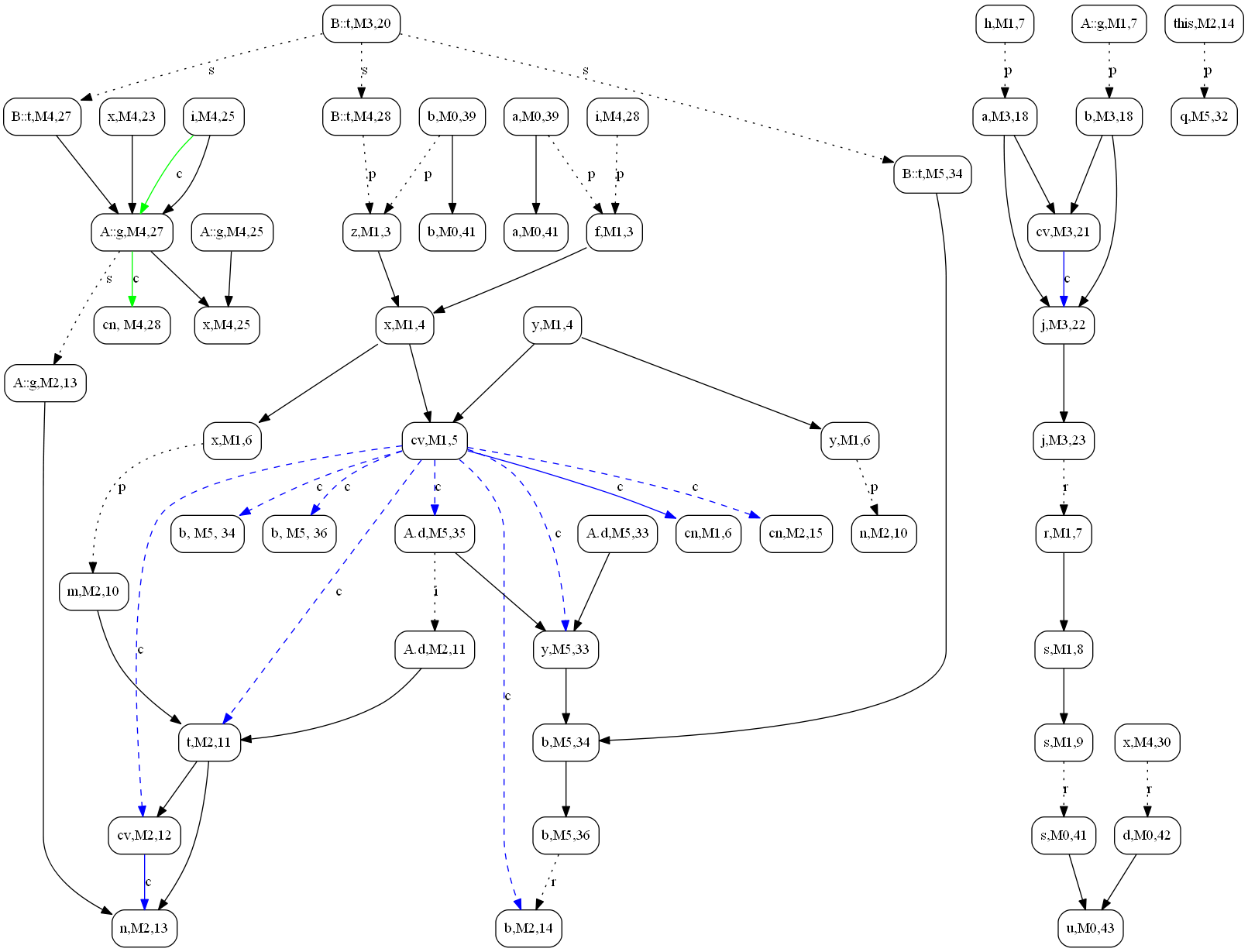
Note:

This diagram is a conceptual illustration only;

The actual dependence graph that Diver created and used for impact analysis is based on the Soot Jimple IR (an immediate representation of Java code transformed from the Java byte-code).